化工原理U3

第三章 机械分离与固体流态化

一、沉降 ⭐

1. 重要概念

• 自由沉降：颗粒在稀相体系中沉降，颗粒间相互干扰可忽略；颗粒相对于流体达到稳定运动时的相对速度称为自由沉降速度（或终端沉降速度）$u_t$。
• 沉降速度 $u_t$：颗粒相对流体的稳定沉降速度（重点强调其本质为“颗粒与流体的相对运动速度”）。
• 影响沉降速度的因素：颗粒粒径、颗粒与流体密度差、流体黏度、流动状态（雷诺数）、颗粒形状等（按教材条目理解即可）。
• 离心分离因素：以离心场替代重力场增大“有效加速度”，提高分离驱动力（仅作概念性认识，具体以后续设备章节展开）。

---

2. 自由沉降与自由沉降速度

对球形颗粒，在重力场中达到稳定沉降时，受力平衡为：

$$\frac{\pi}{6}d_p^3(\rho_p-\rho)g = F_D$$

曳力用曳力系数 $\zeta_D$ 表示：

$$F_D=\zeta_D\cdot\frac{\pi d_p^2}{4}\cdot\frac{\rho u_t^2}{2}$$

由此得到自由沉降速度的通式：

$$u_t=\sqrt{\frac{4d_p(\rho_p-\rho)g}{3\rho\zeta_D}}$$

其中：

• $d_p$：颗粒直径
• $\rho_p,\rho$：颗粒密度、流体密度
• $\mu$：流体动力黏度
• $g$：重力加速度
• $\zeta_D$：曳力系数（随 $Re_p$ 变化）

颗粒雷诺数定义为：

$$Re_p=\frac{\rho u_t d_p}{\mu}$$

---

3. 曳力系数 $\zeta_D$ 与雷诺数 $Re_p$ 的关系（分区经验式）

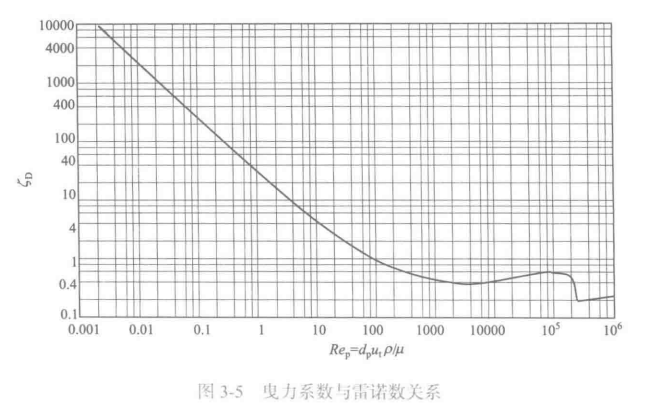
重点曲线可分为三个常用区间（以球形颗粒为准）：

1）斯托克斯区（层流区）：$Re_p\le 0.3$（工程上常近似用于 $Re_p\le 2$）

$$\zeta_D=\frac{24}{Re_p}$$

2）阿伦区（过渡区）：$2<Re_p\le 500$

$$\zeta_D=\frac{18.5}{Re_p^{0.6}}$$

3）牛顿区（湍流区，除边界层外）：$500<Re_p<1\times 10^5$

$$\zeta_D\approx 0.44$$

当 $Re_p>1\times 10^5$ 时，边界层内也出现湍流，$\zeta_D$ 会出现突降并呈不规则变化（通常不作为本章工程计算的常用区间）。

---

4. 自由沉降速度 $u_t$ 的最终结论（3 个常用表达式）⭐

将上述 $\zeta_D(Re_p)$ 代入通式

$$u_t=\sqrt{\frac{4d_p(\rho_p-\rho)g}{3\rho\zeta_D}}$$

得到分区表达式：

（1）层流区：$Re_p\le 2$（重点）⭐

$$u_t=\frac{d_p^2(\rho_p-\rho)g}{18\mu}$$

（2）过渡区：$2<Re_p\le 500$

$$u_t=0.27\sqrt{\frac{d_p(\rho_p-\rho)g\,Re_p^{0.6}}{\rho}}$$

（3）湍流区：$500<Re_p<1\times10^5$

$$u_t=1.74\sqrt{\frac{d_p(\rho_p-\rho)g}{\rho}}$$

---

5. 降尘室（沉降室）的分离条件与处理能力（与 $u_t$ 的关系）

设沉降室长度为 $L$，有效沉降高度为 $H$，气体（或液体）在室内的平均水平速度为 $u$。要求能被完全去除的颗粒满足“停留时间=沉降时间”：

$$\frac{L}{u}=\frac{H}{u_t}$$

处理能力（体积流量）可表示为：

$$V_s=u_{t,\min}A_{\text{底}}$$

其中 $A_{\text{底}}$ 为沉降室底面积，$u_{t,\min}$ 为需要完全去除的最小沉降速度（对应临界粒径），其数值应按上节 $u_t$ 的分区表达式并结合 $Re_p$ 条件确定。

---

6. 降尘室 ⭐

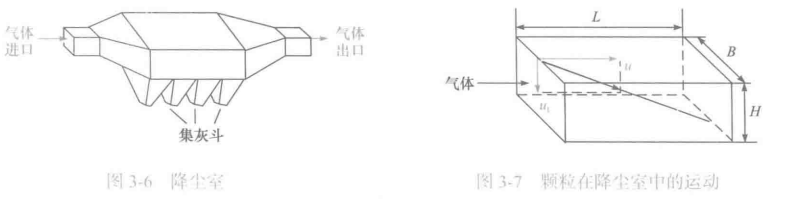
降尘室用于气固体系的重力沉降分离。重点给出“能 100% 去除的最小颗粒”的分离条件：

停留时间（气体在室内）等于沉降所需时间：

$$\frac{L}{u}=\frac{H}{u_t}$$

• $L$：降尘室长度；
• $H$：有效沉降高度；
• $u$：气体在室内的平均水平速度；
• $u_t$：颗粒沉降速度。

气体处理能力（重点结论）：

$$V_s=u_{t,\min}A_{\text{底}}$$

其中 $A_{\text{底}}$ 为降尘室底面积，$u_{t,\min}$ 为需要实现分离的最小沉降速度（对应临界粒径）。重点指出：$V_s$ 与底面积成正比，与高度无关。

---

二、过滤 ⭐

1. 重要概念

• 过滤（filtration）：以多孔介质为分离界面，在压差推动下使流体通过、固体颗粒被截留的机械分离过程。
• 滤浆（slurry）：含固体颗粒的悬浮液（固-液两相体系）。
• 滤液（filtrate）：通过过滤介质后的液体。
• 滤饼（filter cake）：被截留并堆积在过滤介质表面形成的多孔固体层。
• 过滤介质（filter medium）：支承滤饼并允许滤液通过的多孔材料（滤布、滤网、烧结材料等）。
• 过滤推动力：过滤两侧的压差 $\Delta p$（可由加压、真空、液柱静压等形成）。
• 过滤阻力：由滤饼阻力与过滤介质阻力共同构成，且通常随滤饼增厚而增大。
• 过滤速率（以体积通量表征）：

  $$u=\frac{1}{A}\frac{\mathrm{d}V}{\mathrm{d}\tau}$$

  其中 $u$ 为过滤速率（体积通量），$A$ 为过滤面积，$V$ 为滤液体积，$\tau$ 为过滤时间。
• 滤饼比阻 $r$（或 $r_0$）：表征单位厚度滤饼对流动的阻力特性，受颗粒形状、粒径分布、空隙结构及可压缩性影响。
• 可压缩滤饼与不可压缩滤饼：若滤饼结构随 $\Delta p$ 增大而显著致密化，称可压缩滤饼；反之称不可压缩滤饼。
• 压缩指数 $s$（表征滤饼可压缩性）：

  $$r=r_0\,\Delta p^{\,s}$$

  其中 $s=0$ 对应不可压缩滤饼；可压缩滤饼常有 $s>0$（重点给出范围 $s=0.2\sim0.8$）。
• 当量直径 $d_e$：

  $$d_e=\frac{4 *流通截面积}{湿润周边长}=\frac{4 *细管的流动空间}{细管的全部内表面积}$$

---

2. 过滤基本关系式 ⭐

过滤速率的一般表达式（重点给出形式）：

$$u=\frac{1}{A}\frac{\mathrm{d}V}{\mathrm{d}\tau} =\frac{\Delta p}{r\,\mu\,(L+L_e)}$$

• $\Delta p$：过滤压差（推动力）。
• $\mu$：滤液动力黏度。
• $L$：滤饼厚度（随过滤进行增大）。
• $L_e$：等效介质厚度（将过滤介质阻力折算为“等效滤饼厚度”）。
• $r$：滤饼比阻（可随 $\Delta p$ 改变，见压缩指数关系）。

---

3. 滤饼结构参数

重点涉及的结构量：

• 空隙率 $\varepsilon$：

  $$\varepsilon=\frac{V_{\text{总}}-V_{\text{颗粒}}}{V_{\text{总}}}$$

  其中 $V_{\text{总}}$ 为滤饼总体积，$V_{\text{颗粒}}$ 为固体颗粒体积。

• 比表面积 $a$（重点定义为“颗粒表面积/颗粒体积”）：

  $$a=\frac{\text{颗粒表面积}}{\text{颗粒体积}}$$

• 比阻与结构参数关系（重点给出）：

  $$r=\frac{2C\,a^2(1-\varepsilon)^2}{\varepsilon^3}$$

  其中 $C$ 为与颗粒形状等有关的常数（重点给出符号，不展开推导）。

---

4. 生产能力与（最佳）操作周期

• 间歇过滤的平均生产能力（单位时间滤液量）：

  $$Q=\frac{V}{\tau+\tau_w+\tau_D}$$

  • $V$：每周期获得的滤液体积；
  • $\tau$：过滤时间；
  • $\tau_w$：洗涤时间；
  • $\tau_D$：辅助时间（卸饼、装料、装拆滤布、排液、复位等非过滤时间）。

  重点给出：当等效滤液体积 $V_e=0$ 且 $\tau_D=\tau+\tau_w$ 时，$Q$ 取最大值 $Q_{\max}$（以重点表述为准）。

• 连续过滤的生产能力（重点给出形式）：

  $$Q=\frac{V}{T}=nV=A\sqrt{K\phi n}$$

  其中 $T$ 为每转（或每周期）时间，$n$ 为单位时间循环次数（或转速等表征量）。重点指出：$n$ 增大、有效过滤相位（以 $\phi$ 表征）增大时，$Q$ 增大（符号含义以所用设备定义为准）。

---

5. 恒压过滤方程 ⭐

重点给出恒压过滤条件下的速率表达式：

$$u=\frac{1}{A}\frac{\mathrm{d}V}{\mathrm{d}\tau} =\frac{KA}{2(V+V_e)}$$

• $V_e$：等效滤液体积（将过滤介质阻力折算为等效滤饼阻力所对应的滤液体积；重点指出其与过滤介质性质有关）。
• $K$：过滤常数（重点给出其与滤饼性质、滤浆性质、推动力有关）：

  $$K=\frac{2\Delta p^{\,1-s}}{r_0\,c\,\mu}$$

  • $r_0$：滤饼比阻系数；
  • $c$：滤浆中固体含量（以质量/体积或体积/体积的定义随教材约定；此处仅按重点符号使用）；
  • $\mu$：滤液黏度；
  • $s$：压缩指数。

恒压过滤的体积形式（重点结论）⭐：

$$V^2+2VV_e=KA^2\tau$$

以单位面积滤液量 $q=V/A$、等效量 $q_e=V_e/A$ 表示：

$$q^2+2qq_e=K\tau$$

注意（重点原文）：对板框压滤机和叶滤机，过滤面积为所有框或滤叶截面积的 2 倍。
对板框压滤机、叶滤机，在双面过滤（两侧同时出液）且洗涤为单向贯穿（从一侧进入、穿过全部滤饼、由另一侧排出）的简化模型下，若进一步取
$\Delta p_w\approx\Delta p$、$\mu_w\approx\mu$、洗涤不改变滤饼结构（$r_w\approx r$），并忽略（或认为相同处理）介质/支承层阻力影响，则有

$$\frac{u_f}{u_w}\approx 2$$

$$\frac{\left(\frac{\mathrm{d}V}{\mathrm{d}\tau}\right)_f}{\left(\frac{\mathrm{d}V}{\mathrm{d}\tau}\right)_w}\approx 4$$

其中 $u=(1/A)\,\mathrm{d}V/\mathrm{d}\tau$ 为单位面积通量。
注意：“4 倍”指总体积流率比值，不可直接表述为“过滤速度恒为洗涤速度 4 倍”；当洗涤为双向、$\Delta p_w\neq\Delta p$、$\mu_w\neq\mu$、滤饼可压缩或介质/支承层阻力不可忽略时，上述关系不再适用。

---

6. 恒速过滤方程 ⭐

恒速过滤定义：

$$u=\frac{1}{A}\frac{\mathrm{d}V}{\mathrm{d}\tau}=\text{常数}$$

恒速过滤的体积形式（重点结论）⭐：

$$V^2+VV_e=\frac{K}{2}A^2\tau$$

以 $q=V/A$、$q_e=V_e/A$ 表示：

$$q^2+qq_e=\frac{K}{2}\tau$$

先恒速后恒压（重点给出时间关系）：

$$\tau=\tau_1+\frac{1}{K}\left[(q+q_e)^2-(q_1+q_e)^2\right]$$

其中 $(\tau_1,q_1)$ 为恒速阶段结束点的时间与单位面积滤液量。

洗涤时间（重点给出定义式）：

$$\tau_w=\frac{V_w}{\left(\frac{\mathrm{d}V}{\mathrm{d}\tau}\right)_w}$$

其中 $V_w$ 为洗涤液用量，$\left(\frac{\mathrm{d}V}{\mathrm{d}\tau}\right)_w$ 为洗涤阶段的滤液（或洗涤液）体积流率。

---

7. 过滤设备（结构与特点：只作要点性概述）

重点要求掌握的典型设备：

• 板框压滤机：间歇操作；滤饼形成与卸除依赖周期切换；适用于滤饼易形成且需较高澄清度场合。
• 叶滤机：过滤元件为滤叶；可间歇或半连续；过滤面积利用率高（注意过滤面积的定义，见恒压方程备注）。
• 转筒真空过滤机：连续操作；通过转筒分区实现过滤、洗涤、脱液、卸饼等过程。

重点给出：转筒过滤机的过滤时间满足

$$T=\frac{\phi}{n}$$

其中 $\phi$ 为有效过滤相位对应角度（或其无量纲表示），$n$ 为转速（或单位时间转数）。

---

三、旋风分离器

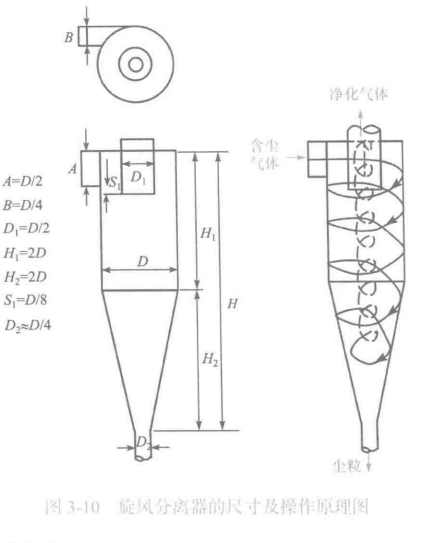
1. 临界直径

旋风分离器以旋转流场产生的离心效应实现气固分离。重点给出临界直径表达式：

$$d_c=\sqrt{\frac{9\mu B}{\pi N u_i\rho_p}}$$

• $d_c$：临界直径（切割粒径；用于表征旋风分离器对粒径的分离界限特征，具体工程判据以教材对“临界/切割”定义为准）；
• $\mu$：气体动力黏度；
• $B$：与结构尺寸有关的特征量（重点以符号出现，按教材对应结构定义使用）；
• $N$：气体在旋风器内的有效旋转圈数（或等效旋转次数）；
• $u_i$：入口气速；
• $\rho_p$：颗粒密度。

---

2. 分离效率

• 粒级效率：针对某一粒径区间颗粒的捕集效率（定义为该粒级被捕集质量分率）。
• 总效率：对入口颗粒粒径分布加权后的总体捕集效率。

工程计算时，总效率通常由粒级效率与粒径分布共同确定（符号与具体计算式按教材给定口径使用）。

---

四、固体流态化

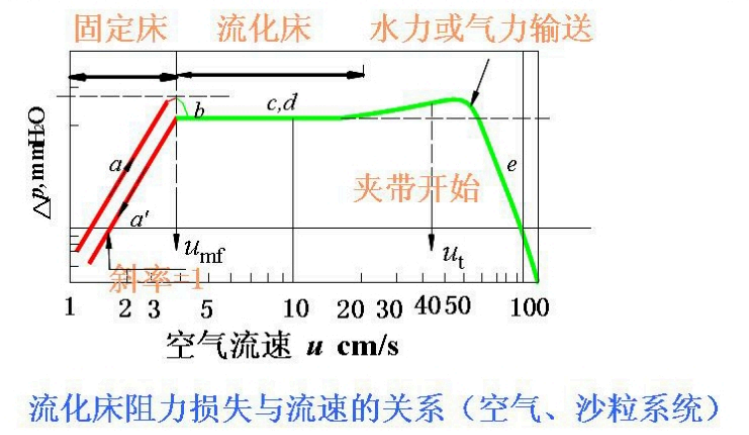
1. 流态化的阶段及主要特征

当流体自下而上通过颗粒床层，随着表观流速 $u$ 增大，床层状态依次表现为：

• 固定床阶段：颗粒基本不动，床层压降随 $u$ 增大而增大。
• 最小流化点：床层开始整体松动并呈流化状态，其对应流速为 最小流化速度 $u_{mf}$。
• 流化床阶段：床层呈流体化外观特征，床层压降在一定范围内近似保持恒定（重点：恒定的广义压差）。
• 夹带与输送阶段：当 $u$ 足够大，颗粒被大量夹带上升，进入气力/液力输送特征区间；重点图中以终端速度 $u_t$ 与夹带开始区分。

---

2. 流化床的主要性质（重点条目）

• 液体样特性：床层可表现出类似液体的宏观行为（如流动性、表面形态变化等），用于强化传热、传质及颗粒处理过程。
• 恒定的广义压差：在流化床稳定流化区间内，床层压降随流速变化不显著（按重点图示规律理解）。

---

3. 聚式流化床的两种不正常现象

• 腾涌现象（slugging）：床层出现大尺度气泡/空隙团块上升，导致床层周期性大幅波动，影响操作稳定性与传递过程。
• 沟流现象（channeling）：流体在床层内形成稳定通道，局部短路，导致床层大部分区域未充分流化，降低有效接触与均匀性。

---

本章要点（对应重点主线）

1. ⭐ 过滤速率由推动力 $\Delta p$ 与阻力（滤饼、介质）共同决定；滤饼可压缩性以 $r=r_0\Delta p^{\,s}$ 表征。
2. ⭐ 恒压过滤与恒速过滤的积分方程分别给出 $V$（或 $q$）与时间 $\tau$ 的关系；$V_e$（或 $q_e$）用于表征介质阻力的等效影响。
3. ⭐ 沉降在层流区可用斯托克斯公式；降尘室以“停留时间=沉降时间”建立分离条件，处理能力与底面积相关。
4. 旋风分离器以临界直径表征分离界限，并以粒级效率与总效率评价分离效果。
5. 固体流态化随流速变化经历固定床、最小流化、流化床及夹带输送等阶段；聚式流化床需关注腾涌与沟流等不正常现象。