第五章 化学平衡
约定:化学计量数 νi(生成物为正、反应物为负),反应进度 ξ;活度 ai 取无量纲形式;标准态用上标 ∘ 表示。
§5.1 摩尔反应吉布斯函数与化学反应方向
1)反应进度(extent of reaction)
2)摩尔反应吉布斯函数(反应吉布斯能)
- 基本热力学关系:
dG=−SdT+Vdp+i∑μidni
- 恒温恒压(T,p 不变):
(∂ξ∂G)T,p=i∑μi(∂ξ∂ni)T,p=i∑νiμi
- 定义摩尔反应吉布斯函数:
ΔrGm≡(∂ξ∂G)T,p=i∑νiμi
3)反应方向与平衡判据
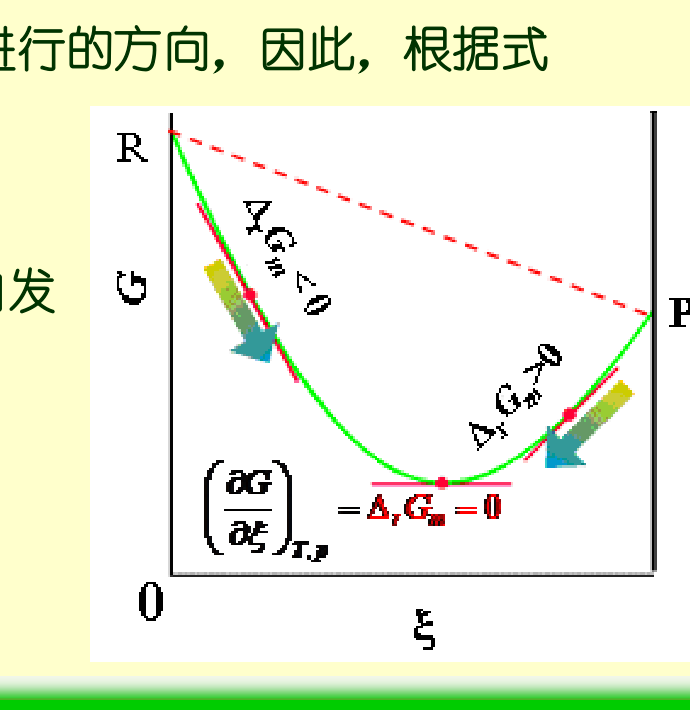
- ΔrGm<0:正向自发(ξ 增大)
- ΔrGm>0:逆向自发(ξ 减小)
- ΔrGm=0:化学平衡
- 恒 T,p 时平衡对应 G(ξ) 的极小值
§5.2 化学反应等温方程与标准平衡常数
1)化学势与活度
2)反应商(reaction quotient)
3)化学反应等温方程(reaction isotherm)
4)标准平衡常数
§5.3 不同反应体系的标准平衡常数(活度/标准态的选取)
1)为什么必须用活度
- 只有用活度定义的 Q、K∘ 才能保证 K∘ 无量纲,并与非理想(逸度、活度系数)相容
2)常见体系的活度(记忆表)
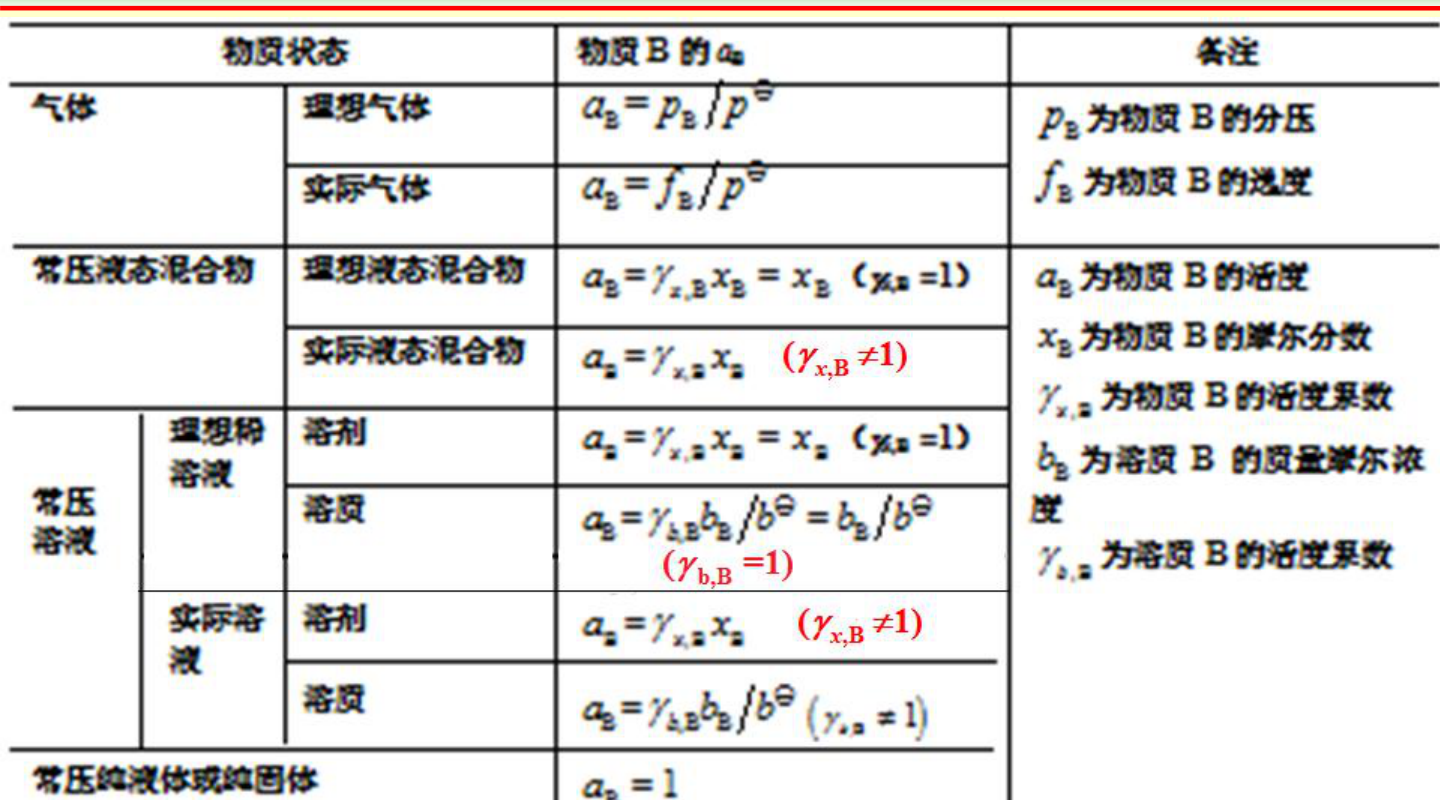
- 常用结论(配合上表):
- 纯液体、纯固体:常取 ai=1
- 理想气体:ai=pi/p∘
- 真实气体:ai=fi/p∘,且 fi=φiyip
- 理想溶液(Raoult 标准态):ai=xi;真实溶液:ai=γixi
- 稀溶液溶质(Henry 标准态):常写 ai=γixi,或用 b(molality)表示
§5.4 平衡常数的不同表示方法(Kp,Kx,Kc,Kb,Kn)
各种 K 的写法本质上都在表达同一个 K∘;差别来自用什么物理量去近似活度、以及是否做了无量纲化。
设一般气相反应写作:
eE+fF⇌yY+zZ
并记
B∑νB≡Δν(对气相物种求和)
1)理想气体:用分压表示的 Kp
- 理想气体活度 ai=pi/p∘:
Kp≡i∏(p∘pi)νi
- 课件关系(对应 K∘ 的无量纲版本):
K∘=Kp∘,Kp∘=Kp(p∘)−∑BνB
2)理想气体:用摩尔分数表示的 Kx
- pi=yip:
K∘=(p∘p)∑BνBKx,Kx≡i∏yiνi
3)理想气体:用浓度表示的 Kc
- 理想气体 pi=ciRT:
K∘=(p∘RT)∑BνBKc
- 若再定义无量纲浓度平衡常数
Kc∘≡Kc(c∘)−∑BνB,
则K∘=(p∘c∘RT)∑BνBKc∘
4)稀溶液:用质量摩尔浓度表示的 Kb
- 定义(b 为 molality):
Kb≡(bE)e(bF)f(bY)y(bZ)z=B∏(bB)νB
- 定义无量纲形式:
Kb∘≡B∏(b∘bB)νB=Kb(b∘)−∑BνB
5)用“物质的量”表示的 Kn
- 定义:
Kn≡(nE)e(nF)f(nY)y(nZ)z=B∏(nB)νB
- 课件给出的关系式:
K∘=[p∘∑BnBp]∑BνBKn
6)课件的“一行总关系式”
- 不同表示之间(理想气体):
Kp=K∘(p∘)∑BνB=Kxp∑BνB=Kc(RT)∑BνB=Kn(∑BnBp)∑BνB
- 若 ∑BνB=0,则:
K∘=Kp=Kx=Kc=Kn
§5.5 标准平衡常数 K∘ 的求取(热化学/电化学数据)
1)由 ΔrGm∘ 求 K∘
K∘=exp(−RTΔrGm∘)
若有标准生成吉布斯能:
ΔrGm∘=i∑νiΔfGm,i∘
2)由 ΔrHm∘,ΔrSm∘ 求 K∘
ΔrGm∘=ΔrHm∘−TΔrSm∘
其中
ΔrHm∘=i∑νiΔfHm,i∘,ΔrSm∘=i∑νiSm,i∘
3)由电动势求 K∘
- 可逆电池:
ΔrGm=−nFE,ΔrGm∘=−nFE∘
- 联立:
K∘=exp(RTnFE∘)
§5.6 温度对标准平衡常数的影响(Van’t Hoff)
1)从 Gibbs–Helmholtz 推到 van’t Hoff(课件推导链)
- Gibbs–Helmholtz(对标准反应量):
(∂T∂(ΔrGm∘/T))p=−T2ΔrHm∘
- 又 ΔrGm∘=−RTlnK∘,所以
TΔrGm∘=−RlnK∘
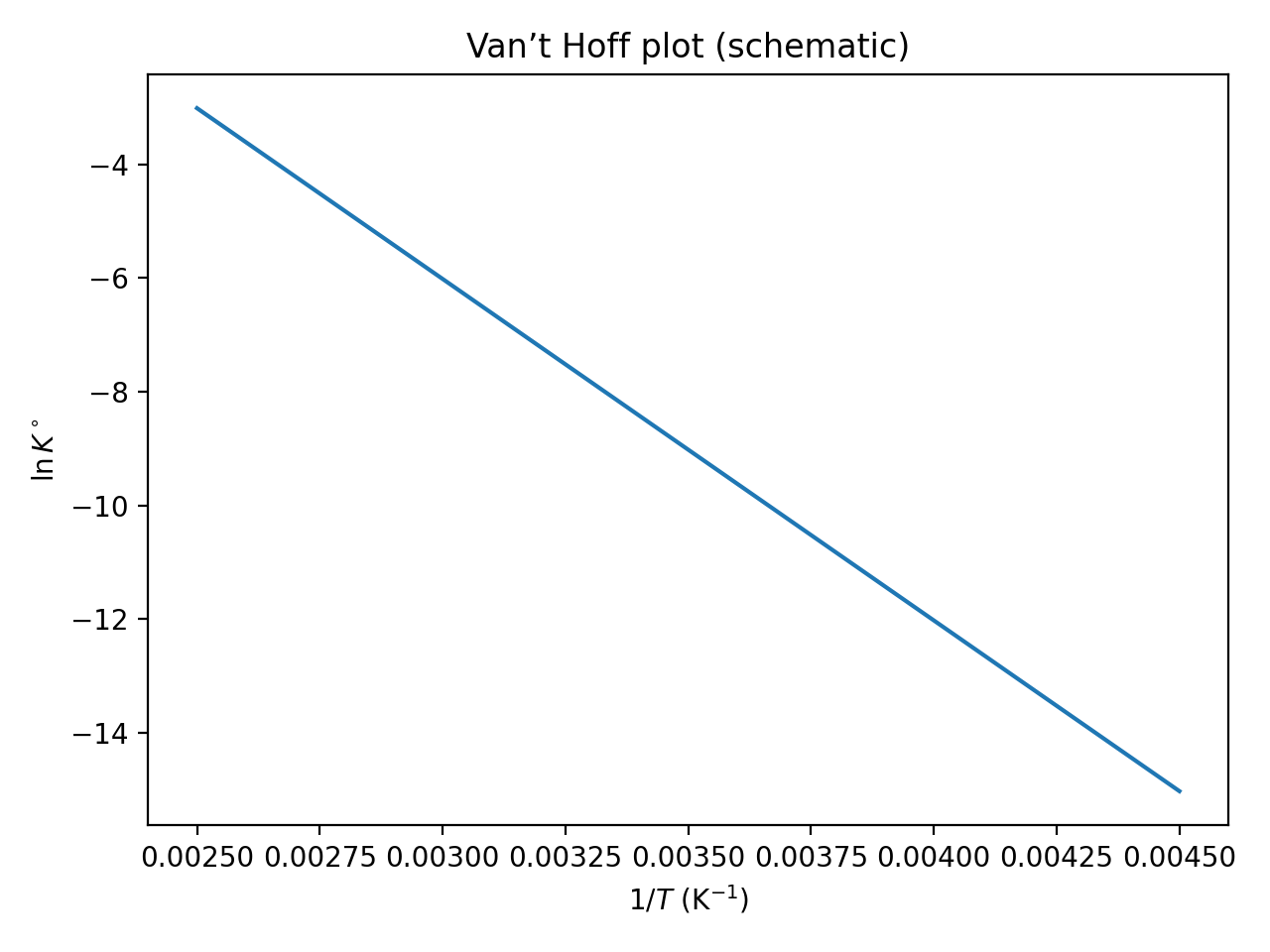
代入得:dTdlnK∘=RT2ΔrHm∘
2)积分形式(近似 ΔrHm∘ 常数)
lnK1∘K2∘=−RΔrHm∘(T21−T11)
3)定性判断(课件结论)
- ΔrHm∘>0(吸热):T↑⇒K∘↑
- ΔrHm∘<0(放热):T↑⇒K∘↓
4)Kc∘ 的温度影响(课件式)
- 理想气体有:
ΔrHm∘=ΔrUm∘+ΔνRT
- 因而可得到(课件给出):
dTdlnKc∘=RT2ΔrUm∘
§5.7 其它因素对理想气体反应平衡的影响(用 Q 与 K∘)
- 平衡时 Q=K∘;扰动后比较 Q 与 K∘:
- Q<K∘:正向进行使 Q 增大
- Q>K∘:逆向进行使 Q 减小
1)改变压力/体积(理想气体)
- 恒温压缩(p 增大):
- Δν<0:向气体物质的量更少一侧
- Δν>0:相反
- Δν=0:组成不变
2)加入惰性气体(理想气体)
- 恒容加入:各 pi=niRT/V 不变,Q 不变,平衡不移动
- 恒压加入:V 变大、各 pi 变小,Q 改变,平衡移动由 Q 与 K∘ 判定
3)催化剂
- 不改变 K∘ 与平衡组成,只改变达到平衡的速率
4)改变组成(加反应物/移走生成物)
- 直接改变 Q,方向由 Q 与 K∘ 比较决定
本章一页“总公式”
- 反应吉布斯函数:
ΔrGm=i∑νiμi
- 化学势与活度:
μi=μi∘+RTlnai
- 反应商与等温方程:
Q=i∏aiνi,ΔrGm=ΔrGm∘+RTlnQ
- 平衡常数:
ΔrGm∘=−RTlnK∘
- van’t Hoff:
dTdlnK∘=RT2ΔrHm∘



