第四章 多组分系统热力学
本章核心:用“偏摩尔量/化学势”描述多组分体系;用“逸度/活度”把真实体系化学势写成与理想体系同型的对数形式;用“依数性”把稀溶液重要现象统一起来。
§4.1 组成表示与基本概念
多组分体系:组分数为 C,第 i 个组分的物质的量 ni,总量 n=∑ini。
摩尔分数:
xi=nni,i∑xi=1
常用浓度标度(依体系选择):
- 质量分数 wi
- 质量摩尔浓度(molality)bi(或 mi)
- 体积摩尔浓度(molarity)ci
气体混合物中(理想气体近似):分压 pi=yip,其中 yi 为气相摩尔分数。
§4.2 偏摩尔量(Partial molar property)
1)定义(广度量的“边际贡献”)
对任一广度性质 M(如 V,H,S,G,…),组分 i 的偏摩尔量定义为:
Mˉi=(∂ni∂M)T,p,nj=i
物理含义:在 T,p 与其他组分物质的量不变时,向体系“微量加入”组分 i,体系总性质 M 的变化率。
2)欧拉关系(总量可由偏摩尔量叠加)
若 M 对各 ni 为一阶齐次,则:
M=i∑niMˉi
典型例子(体积):
V=i∑niVˉi
3)二元体系的作图法(切线截距法)
对二元体系(1/2),先将摩尔性质写成 Mm=M/n 并视作组成函数(如 x2)。则
Mˉ1=Mm−x2(∂x2∂Mm)T,p,Mˉ2=Mm+x1(∂x2∂Mm)T,p
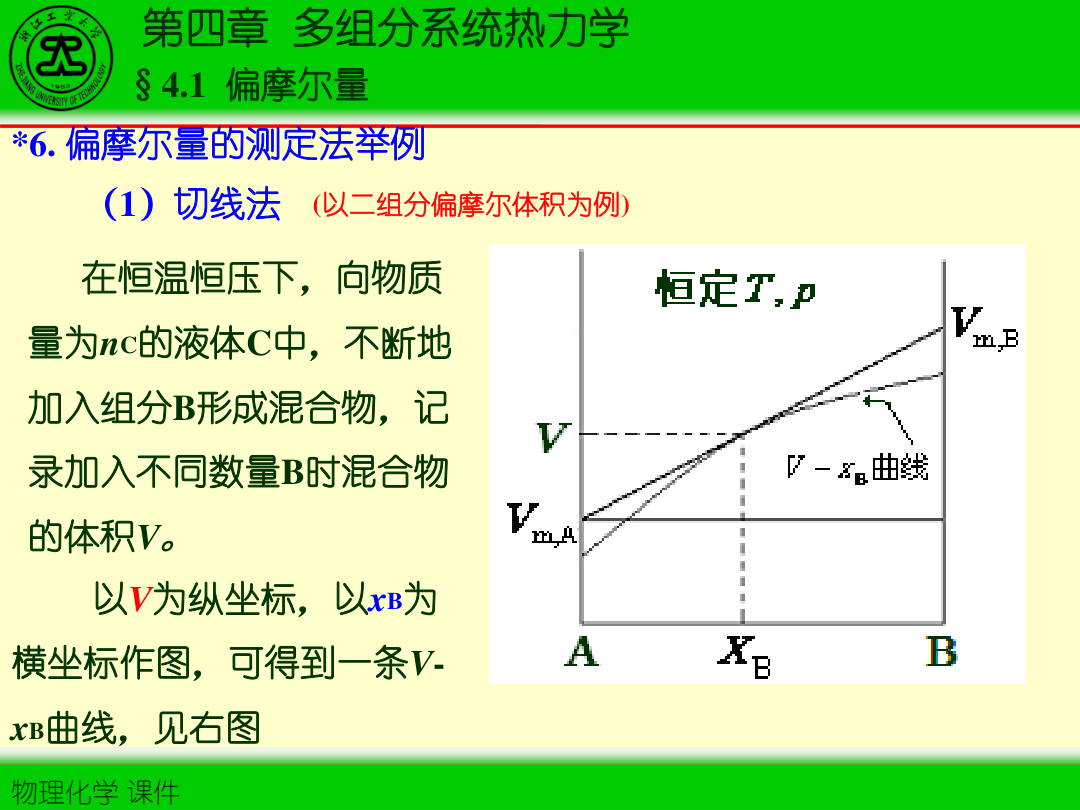
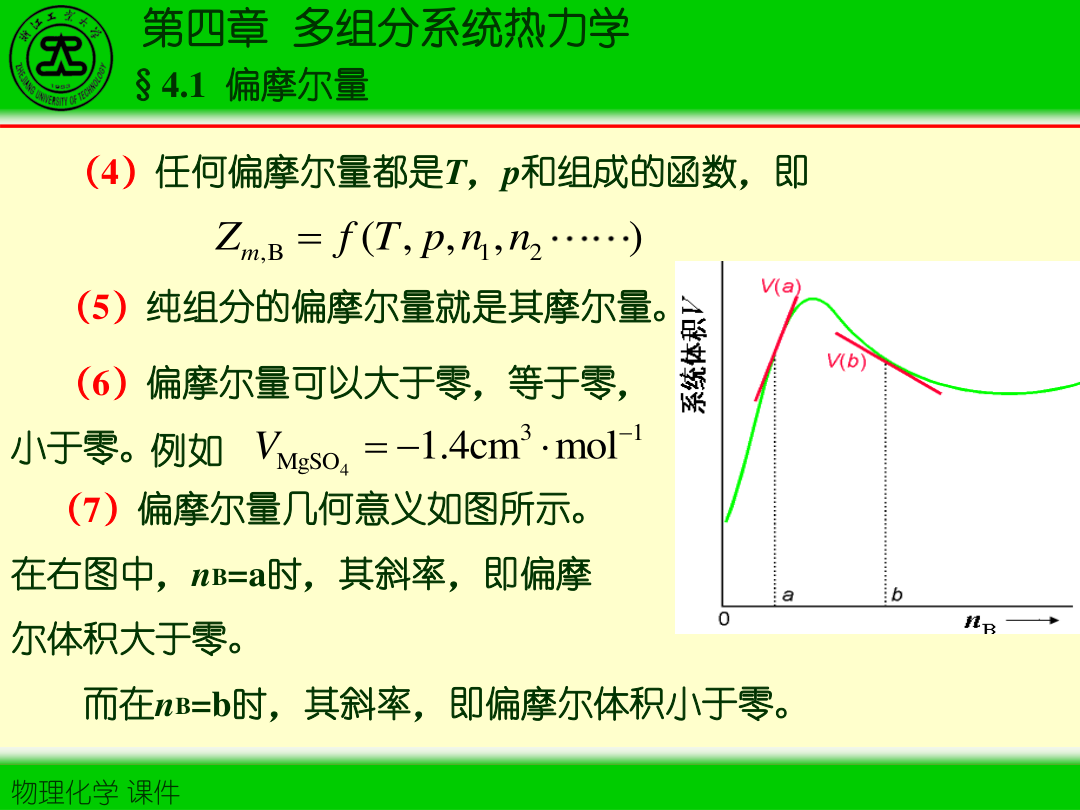
4)Gibbs–Duhem 关系(偏摩尔量不独立)
在 T,p 恒定时:
i∑nidMˉi=0⟺i∑xidMˉi=0
§4.3 化学势(Chemical potential)
1)定义:吉布斯函数的偏摩尔量
μi=(∂ni∂G)T,p,nj=i=Gˉi
2)多组分体系的基本微分式
dG=−SdT+Vdp+i∑μidni
并有:
(∂T∂μi)p,n=−Sˉi,(∂p∂μi)T,n=Vˉi
3)平衡判据(最常用“相等条件”)
两相平衡(同一组分在两相中化学势相等):
μi(α)=μi(β)
3)化学势与温度、压强关系
由2)可知:
(∂T∂μi)p,n=−Sˉi<0,(∂p∂μi)T,n=Vˉi>0
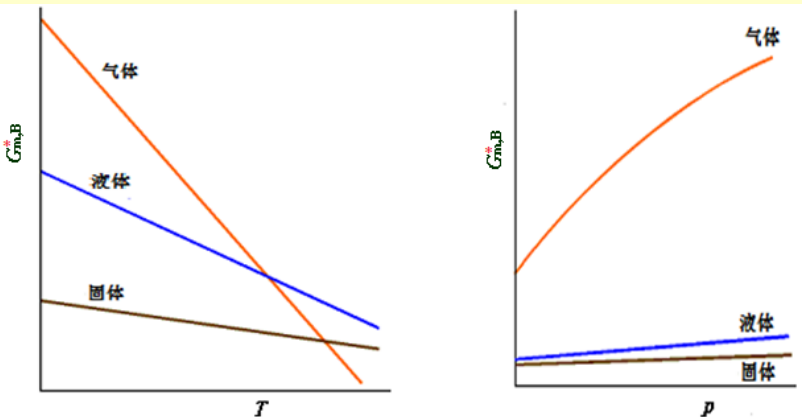
故μ随温度增高而降低,随压强增加而增大。
纯物质系统, μ与T、
p的关系图示可参见
图Gm,B与T、p 关系的
图示。
§4.4 逸度与逸度系数(Fugacity)
1)为什么要引入逸度?
目标:让真实气体(或混合气)化学势也能写成与理想气体同型的对数形式。
2)用逸度写化学势
纯物质(气相):
μ(T,p)=μ∘(T)+RTlnp∘f
混合物中组分 i(气相):
μi(T,p,{y})=μi∘(T)+RTlnp∘fi
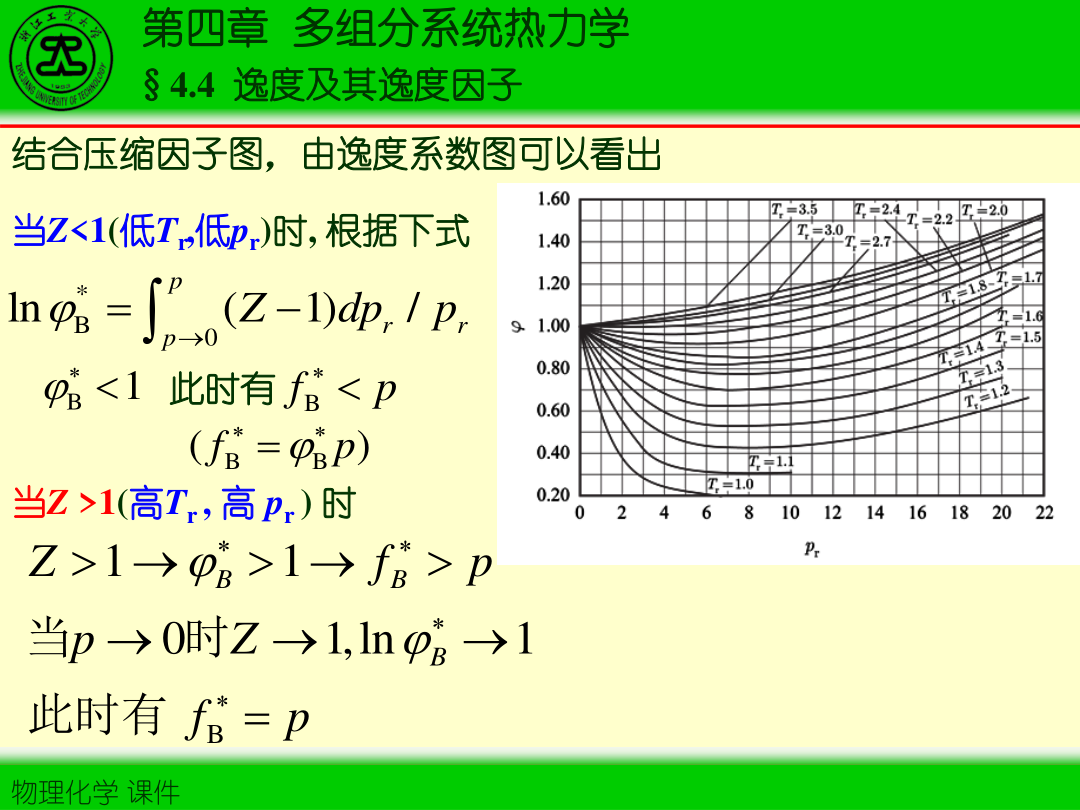
逸度系数(纯气体):
φ=pf
混合气中组分逸度系数:
φi=yipfi
当 p→0:f→p, φ→1(理想极限)。
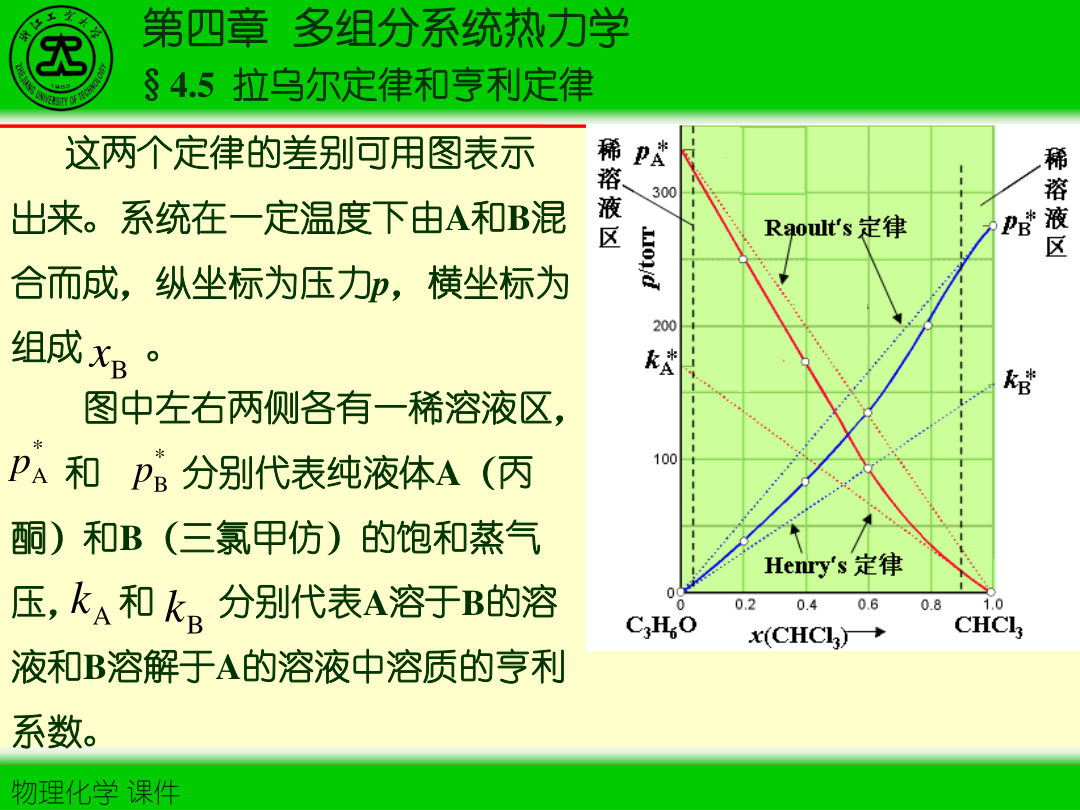
§4.5 拉乌尔定律与亨利定律
1)拉乌尔定律(溶剂端/理想溶液)
对液相摩尔分数为 xi 的组分,其平衡分压:
pi=xipi∗
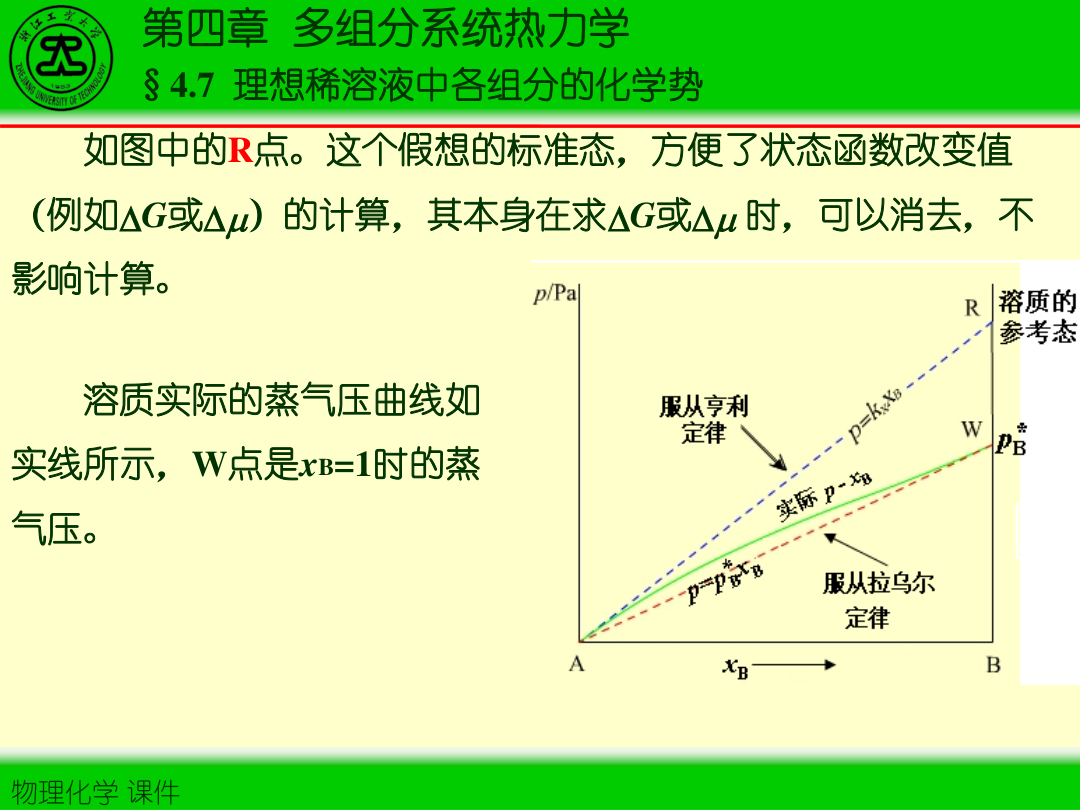
2)亨利定律(无限稀释端/溶质端)
稀溶液中挥发性溶质 i:
pi=kx,ixi
3)两定律联系:标准态不同
- 溶剂常取“拉乌尔标准态”(x→1)
- 溶质常取“亨利标准态”(x→0)
§4.6 理想溶液(Ideal solution)
1)理想溶液化学势(液相)
μi=μi∗(T,p)+RTlnxi
2)理想溶液混合函数
ΔGmix=RTi∑nilnxi
ΔSmix=−Ri∑nilnxi
ΔHmix=0,ΔVmix=0
§4.7 活度与活度系数(Activity)
1)用活度统一化学势形式
μi=μi∘+RTlnai
2)常用活度系数形式
以摩尔分数标度(拉乌尔标准态):
ai=γixi
并满足 xi→1 时 γi→1。
3)超额吉布斯函数与活度系数
GE=RTi∑nilnγi
GˉiE=RTlnγi
4)Gibbs–Duhem 对活度系数约束(T,p 恒定)
i∑xidlnγi=0
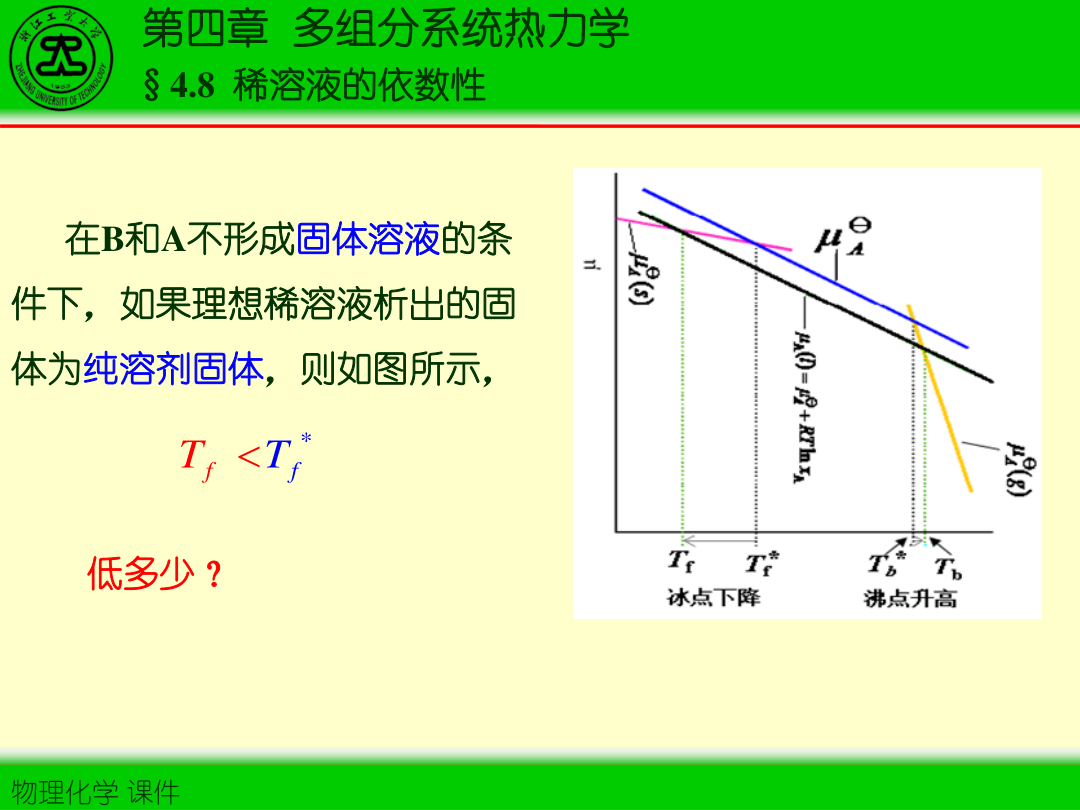
§4.8 稀溶液的依数性(Colligative properties)
1)蒸气压下降(溶质不挥发)
溶剂 A:
pA=xApA∗
相对下降:
pA∗ΔpA=xB
2)沸点升高
ΔTb=KbbB
3)凝固点降低
ΔTf=KfbB
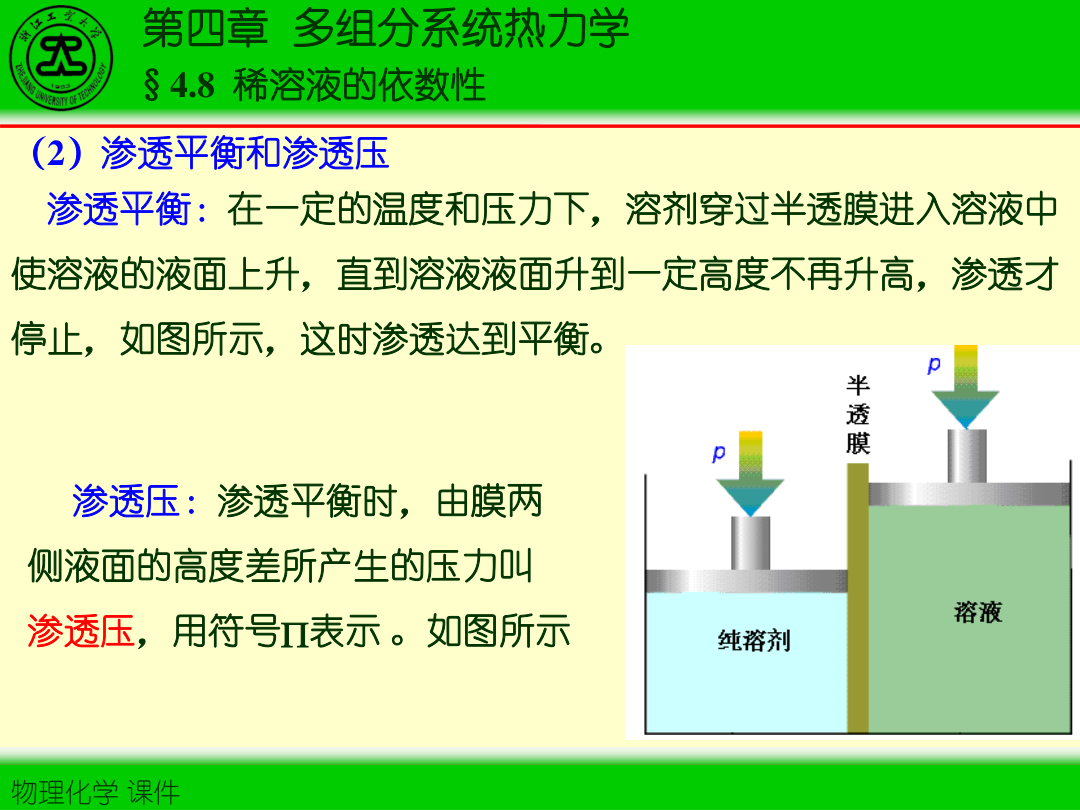
4)渗透压(van’t Hoff 形式)
Π=cBRT
并可写为 ΠV=nBRT。
电解质溶液常引入 van’t Hoff 因子 i:Π=icRT,ΔTb=iKbb,ΔTf=iKfb。
§4.9 相平衡的统一表述(用逸度/活度写“相等条件”)
1)相平衡本质:同组分两相化学势相等
μi(l)=μi(v)
等价地(用逸度):
fi(l)=fi(v)
2)常用工程化写法(计算框架)
气相(真实):
fi(v)=yiφip
液相(活度):
fi(l)=aifi∘且ai=γixi
非理想性集中在 φi(气相)与 γi(液相),便于分模块建模与计算。








