物理化学U3

第三章 热力学第二定律

约定：$Q>0$ 为体系吸热；功 $W$ 取“环境对体系做功为正”。
因此热机对外输出功的大小 $W_{\mathrm{out}}=-W>0$。

---

§3.1 自发过程与不可逆性

• 自发过程：在给定条件下无需外界持续做功即可发生；其逆过程不能自动发生。
• 不可逆性来源：摩擦/黏滞、有限温差传热、自由膨胀、扩散混合、化学反应等（均伴随耗散）。

---

§3.2 第二定律的表述（Kelvin / Clausius）与第二类永动机

• 第二类永动机：从单一热源吸热并把热量全部转变为功且不引起其他变化——不可能实现。
• Clausius 表述：热量不可能自动从低温物体传到高温物体而不引起其他变化。
• Kelvin 表述：不可能制造一种循环热机，使其唯一结果是从单一热源吸热并把吸收的热量全部变为功。
• 两种表述等价（互相可导出）。

---

§3.3 热机、卡诺循环与卡诺定理

1）热机效率

• 热机：从高温热源 $T_h$ 吸热 $Q_h$，向低温热源 $T_l$ 放热 $Q_l$，对外输出功 $W_{\mathrm{out}}$。
• 循环过程 $\Delta U=0$，能量关系：

$$W_{\mathrm{out}}=Q_h+Q_l\qquad (Q_l<0)$$

• 效率定义：

$$\eta=\frac{W_{\mathrm{out}}}{Q_h}=1+\frac{Q_l}{Q_h}\qquad (0<\eta<1,\;Q_l<0)$$

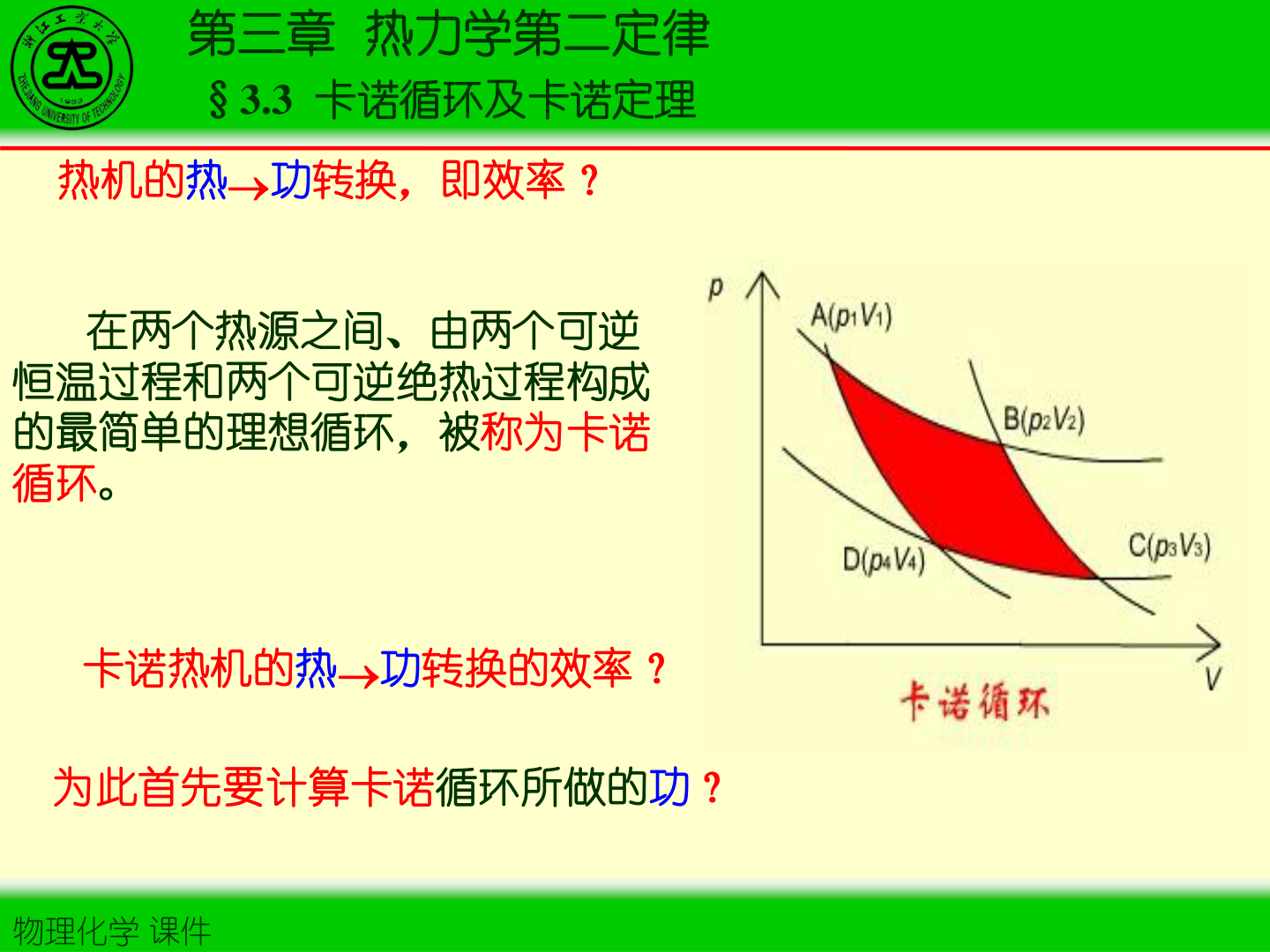
2）卡诺循环（两等温 + 两绝热，可逆）

• 卡诺循环由 2 个可逆等温过程与 2 个可逆绝热过程组成，是理想可逆热机的基准。

3）卡诺效率与卡诺定理

• 卡诺效率（只与两热源温度有关）：

$$\eta_R=1-\frac{T_l}{T_h}$$

• 卡诺定理：
  任意两热源间：可逆热机效率最大；同一对热源间：所有可逆热机效率相同；不可逆热机 $\eta<\eta_R$。

---

§3.4 热力学温标（绝对温标的建立）

• 可逆卡诺机满足：

$$\frac{Q_h}{T_h}+\frac{Q_l}{T_l}=0$$

• 因而：

$$\frac{Q_h}{|Q_l|}=\frac{T_h}{T_l}$$

---

§3.5 克劳修斯不等式与熵的引入

1）克劳修斯不等式

$$\oint\frac{\delta Q}{T}\le 0$$

• 等号：可逆循环；小于号：不可逆循环。

2）熵（状态函数）

• 定义（用可逆过程定义）：

$$dS=\frac{\delta Q_{\mathrm{rev}}}{T}$$

• 一般不等式形式：

$$dS\ge \frac{\delta Q}{T}$$

3）熵增原理

• 孤立系统：

$$\Delta S_{\mathrm{iso}}\ge 0$$

• 系统 + 环境（宇宙）：

$$\Delta S_{\mathrm{univ}}=\Delta S_{\mathrm{sys}}+\Delta S_{\mathrm{surr}}\ge 0$$

• 若环境是温度为 $T$ 的热库：

$$\Delta S_{\mathrm{surr}}=-\frac{Q_{\mathrm{sys}}}{T}$$

---

§3.6 常用熵变计算模板（只列公式）

1）相变熵

$$\Delta S_{\mathrm{tr}}=\frac{\Delta H_{\mathrm{tr}}}{T_{\mathrm{tr}}}$$

2）理想气体熵变（$C_{p,m},C_{V,m}$ 近似常数）

$$\Delta S=nC_{V,m}\ln\frac{T_2}{T_1}+nR\ln\frac{V_2}{V_1}$$

$$\Delta S=nC_{p,m}\ln\frac{T_2}{T_1}-nR\ln\frac{p_2}{p_1}$$

3）混合熵（理想混合）

$$\Delta S_{\mathrm{mix}}=-R\sum_i n_i\ln x_i$$

4）反应熵

$$\Delta_r S=\sum_i \nu_i S_{m,i} \qquad ,\qquad \Delta_r S^\circ=\sum_i \nu_i S_{m,i}^\circ$$

---

§3.7 第三定律与绝对熵

• 第三定律（Planck）：$T\to 0$ 时完全晶体 $S(0)=0$（规定熵零点）。
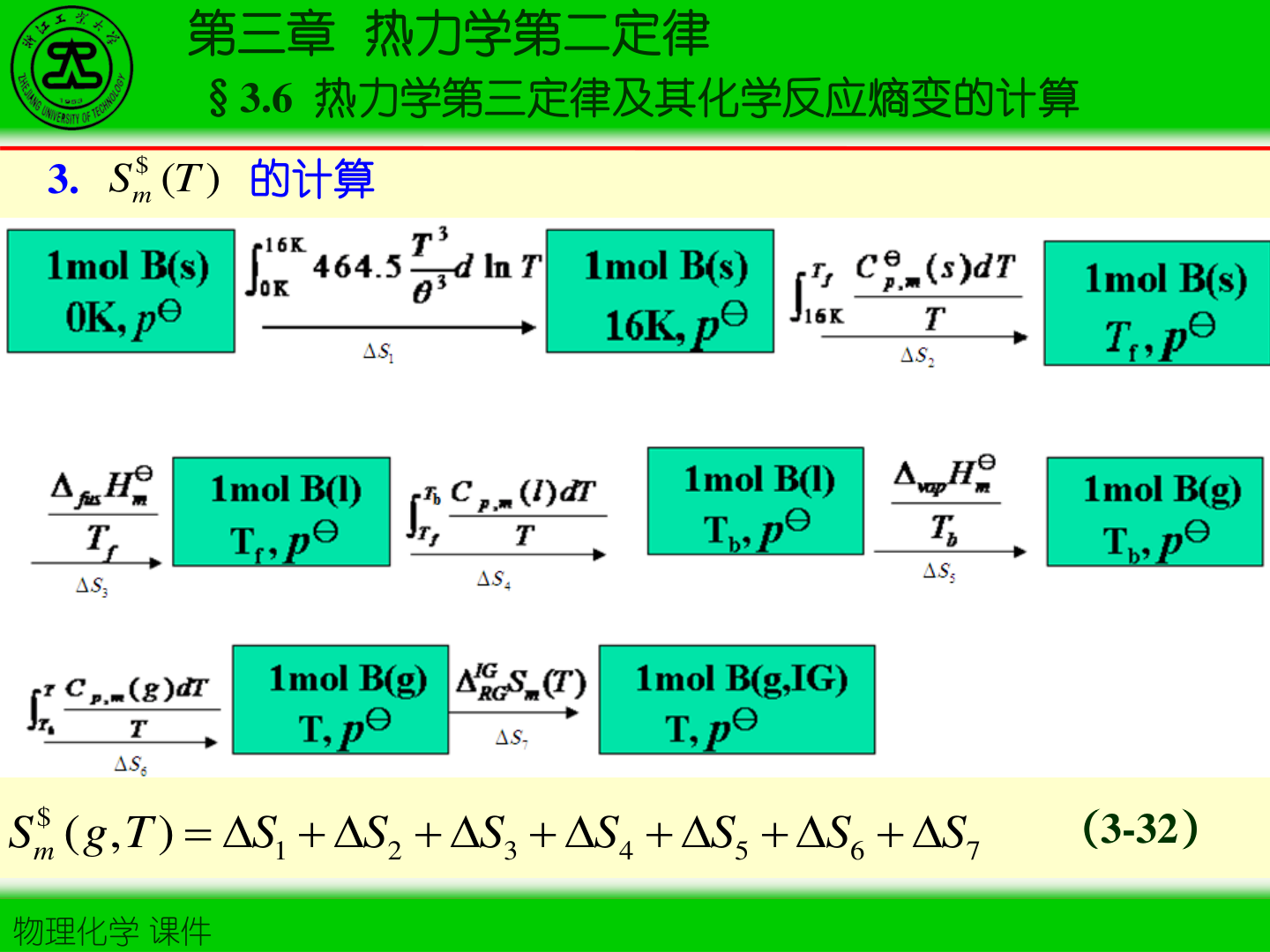
• 绝对熵计算框架（分段积分 + 相变项）：

$$S_m(T)=\int_{0}^{T}\frac{C_{p,m}}{T}\,dT+\sum_k\frac{\Delta H_{\mathrm{tr},k}}{T_{\mathrm{tr},k}}$$

---

§3.8 自由能函数与自发判据（$A/G$）

1）定义

$$A=U-TS,\qquad G=H-TS$$

2）微分式（闭系、仅 $pV$ 功）

$$dA=-S\,dT-p\,dV$$

$$dG=-S\,dT+V\,dp$$

3）“最小值原理”（判据）

• 等温等容：

$$\Delta A\le 0\;(\text{自发}),\quad \Delta A=0\;(\text{平衡})$$

• 等温等压：

$$\Delta G\le 0\;(\text{自发}),\quad \Delta G=0\;(\text{平衡})$$

---

§3.9 Maxwell 关系与 Gibbs–Helmholtz

1）Maxwell 关系（示例两条）

$$\left(\frac{\partial S}{\partial V}\right)_T=\left(\frac{\partial p}{\partial T}\right)_V$$

$$\left(\frac{\partial S}{\partial p}\right)_T=-\left(\frac{\partial V}{\partial T}\right)_p$$

2）Gibbs–Helmholtz

$$\left(\frac{\partial (G/T)}{\partial T}\right)_p=-\frac{H}{T^2}$$

对反应量：

$$\left(\frac{\partial (\Delta_r G^\circ/T)}{\partial T}\right)_p=-\frac{\Delta_r H^\circ}{T^2}$$

---

§3.10 $\Delta G$、平衡常数与温度影响

• 反应 Gibbs 函数：

$$\Delta_r G=\Delta_r G^\circ+RT\ln Q$$

• 平衡：$\Delta_r G=0$，得：

$$K=\exp\!\left(-\frac{\Delta_r G^\circ}{RT}\right)$$

• van’t Hoff：

$$\frac{d\ln K}{dT}=\frac{\Delta_r H^\circ}{RT^2}$$