第二章 热力学第一定律
约定:以下采用课件常用号记
- 系统吸热:Q>0;系统放热:Q<0
- 体积功:δW=−pexdV(膨胀 dV>0⇒W<0;压缩 dV<0⇒W>0)
- 闭合循环:ΔU=0⇒Q=−W
一、热力学基本概念与研究对象
1. 系统、环境与边界
- 系统:研究对象(可为气体/液体/固体/溶液/反应体系等)
- 环境:系统之外的一切
- 边界:系统与环境的分界(可真实或假想)
2. 系统的类型
- 敞开系统:与环境交换物质与能量
- 封闭系统:不交换物质,可交换能量
- 孤立系统:既不交换物质,也不交换能量
3. 状态、状态函数与过程量
- 状态:用一组宏观变量描述(T,p,V,ni,…)
- 状态函数:只与始末态有关(如 U,H,T,p,V)
- 过程量:与途径有关(如 Q,W)
- 数学特征:
- 状态函数:全微分 dU,dH
- 过程量:不完全微分 δQ,δW
4. 过程与路径(常见分类)
- 等温:T=const
- 等压:p=const
- 等容:V=const
- 绝热:δQ=0
- 循环:始态=终态
- 可逆/不可逆:
- 可逆过程:由无穷小驱动力推动,过程可“逆向无痕”返回(理想极限)
- 不可逆过程:存在有限梯度(如有限压差、温差、摩擦等)
二、功与热:能量交换的两种方式
1. 热(Heat)
- 热是由于系统与环境存在温差而发生的能量传递,记为 δQ
- δQ 是过程量(路径函数),不能写成状态函数差
2. 功(Work)
- 功是除热以外的能量传递方式,记为 δW
- 常见形式:
- 体积功(pV功):δW=−pexdV
- 非体积功:电功、表面功、轴功等(做题/推导时需明确是否存在)
3. 体积功的几种典型计算(§2.4)
(1)恒外压膨胀/压缩
W=−pex(V2−V1)
(2)分段恒外压(课件用于对比“途径依赖”)
把膨胀/压缩分成若干段,每段外压近似常数 pex,k,则
W=−k∑pex,k(Vk+1−Vk)
(3)可逆膨胀/压缩(准静态极限)
- 可逆时 pex=p,因此
Wrev=−∫V1V2pdV
(4)理想气体等温可逆膨胀
p=VnRT
Wrev,iso=−∫V1V2VnRTdV=−nRTlnV1V2=nRTlnp1p2
(5)自由膨胀
- 若 pex=0,则 δW=0⇒W=0
三、热力学第一定律(能量守恒)
1. 第一定律(封闭系统)
ΔU=Q+W或dU=δQ+δW
- 内能 U:系统微观能量的总和(状态函数)
- 循环过程:ΔU=0⇒Q=−W
2. 物理意义
- 能量不会凭空产生或消失,只能转化或传递
- 解决问题的核心:
明确过程约束(等温/等压/绝热/是否可逆/是否只做体积功)→ 写能量方程 → 代入 Q,W 表达式
四、恒容热、恒压热与焓
1. 恒容热 QV 与 ΔU
在 封闭体系、恒容、只做体积功(且 dV=0) 情况:
W=−∫pexdV=0
QV=ΔU
2. 焓(Enthalpy)
定义:
H≡U+pV
微分形式:
dH=dU+pdV+Vdp
3. 恒压热 Qp 与 ΔH
在 封闭体系、恒压、且不做非体积功 情况:
Qp=ΔH
注意:只要条件不满足(如有非体积功、非恒压、非封闭等),ΔH 仍有意义,但不再等于 Qp。
五、热容与变温过程的 ΔU,ΔH
1. 热容的定义(过程量)
- 热容本质:单位温度变化所需热量(依赖约束条件)
- 常用:恒容热容 CV、恒压热容 Cp
2. 摩尔热容(常用记号)
CV,m=n1(dTδQ)V=(∂T∂Um)V
Cp,m=n1(dTδQ)p=(∂T∂Hm)p
3. 由热容计算 ΔU,ΔH
一般形式(允许热容随温度变):
ΔU=∫T1T2nCV,m(T)dT
ΔH=∫T1T2nCp,m(T)dT
4. 理想气体的重要结论
- 焦耳实验结论(理想气体):U=U(T)(内能只与温度有关)
推出:等温过程中 ΔU=0;同理 H=H(T),等温 ΔH=0
- Mayer 关系(理想气体):
Cp,m−CV,m=R
γ≡CV,mCp,m
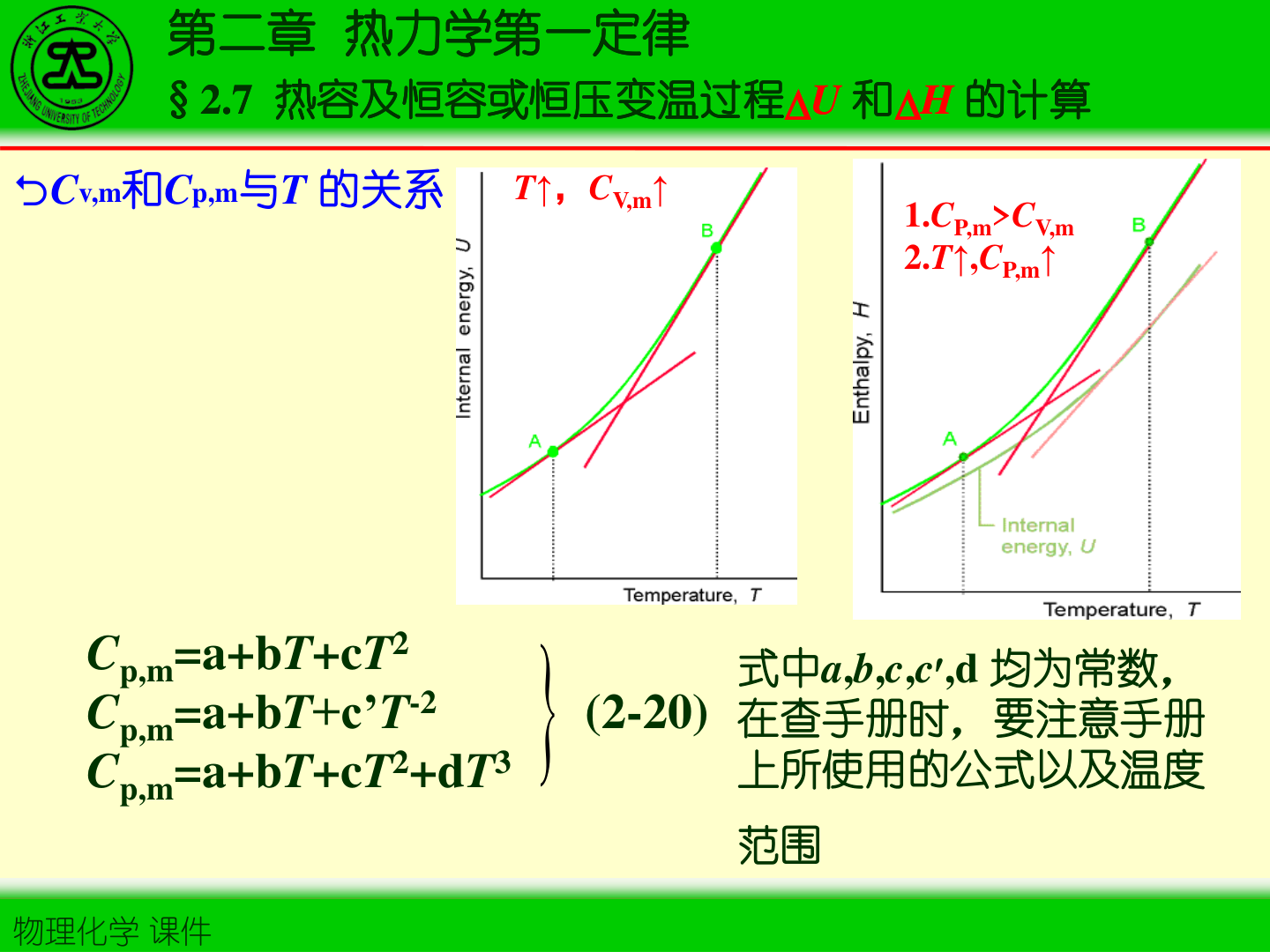
5. 热容随温度的经验表达(查表常见)
Cp,m(T)=a+bT+cT2+dT3(或其它等价形式)
六、理想气体的绝热过程(§2.8)
1. 绝热条件与基本关系
- 绝热:δQ=0
- 第一律:dU=δW
- 理想气体:dU=nCV,mdT
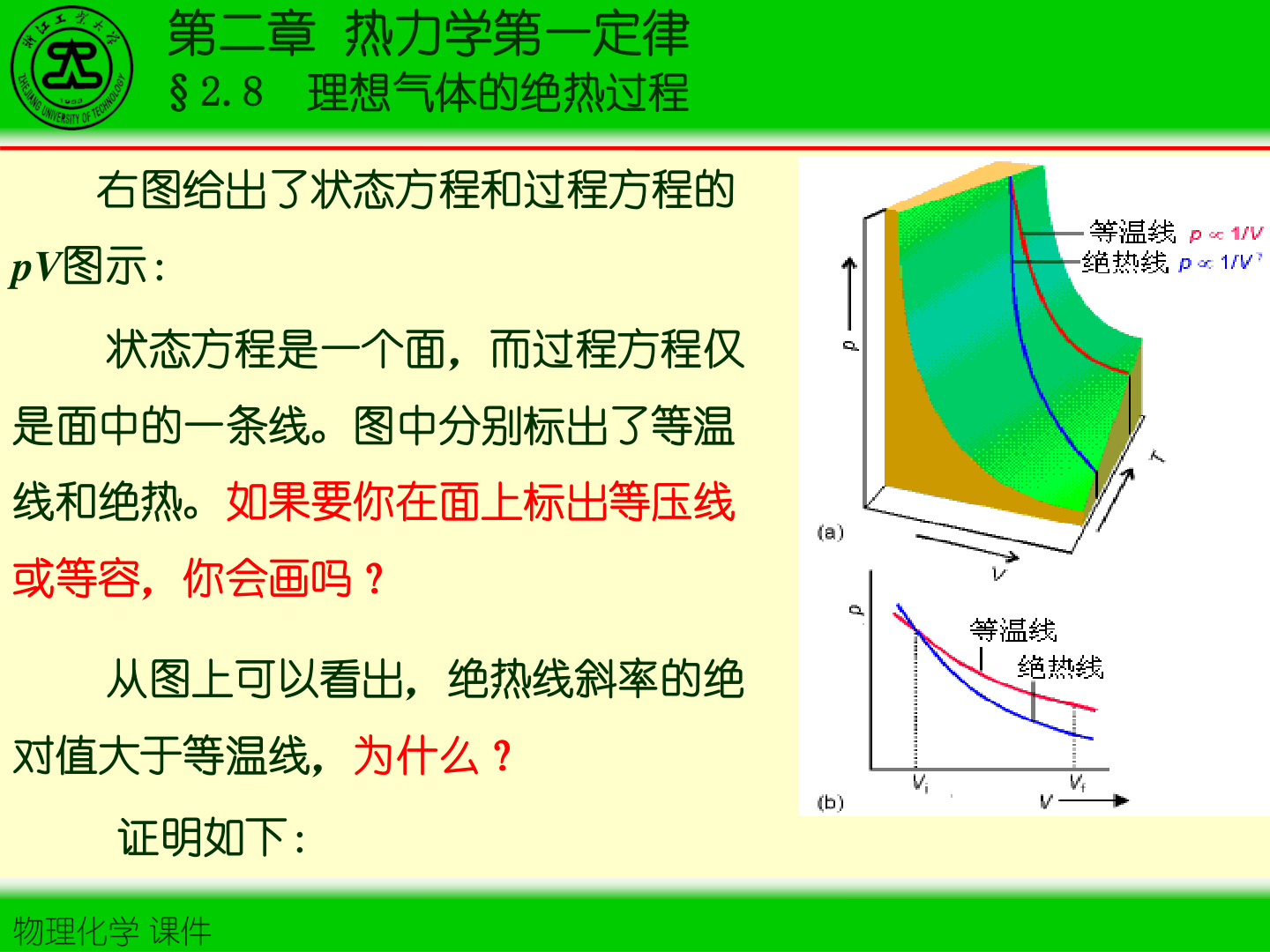
2. 绝热可逆过程方程(泊松方程)
令 γ=Cp,m/CV,m,则
TVγ−1=const(2−27)
结合 pV=nRT 得
pVγ=const(2−28)
Tp(1−γ)/γ=const(2−29)
3. 绝热可逆过程功(理想气体)
Wad,rev=ΔU=nCV,m(T2−T1)
也常写成(等价形式):
Wad,rev=1−γp2V2−p1V1=1−γnR(T2−T1)
4. 方向判断
- 绝热膨胀:W<0, ΔU<0, T↓
- 绝热压缩:W>0, ΔU>0, T↑
七、实际气体的节流膨胀(Joule–Thomson,§2.9)
1. 节流膨胀的定义与特征
- 节流膨胀:气体通过多孔塞/阀门等产生压降的绝热过程(始、终态压力分别保持恒定)
- 典型热力学结论:等焓过程
ΔH=0
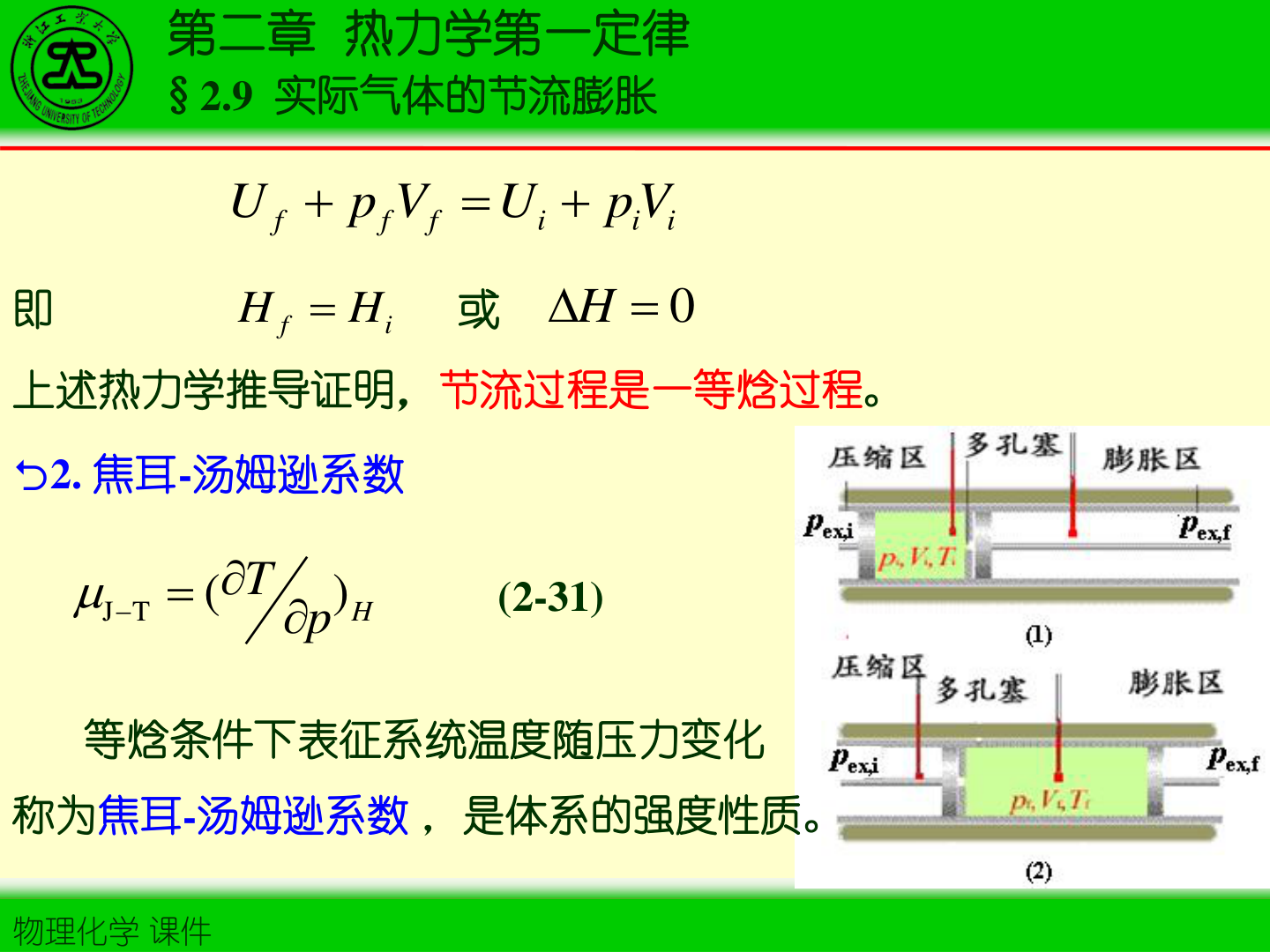
2. 焦耳–汤姆逊系数
定义:
μJ−T≡(∂p∂T)H
判据(节流时 dp<0):
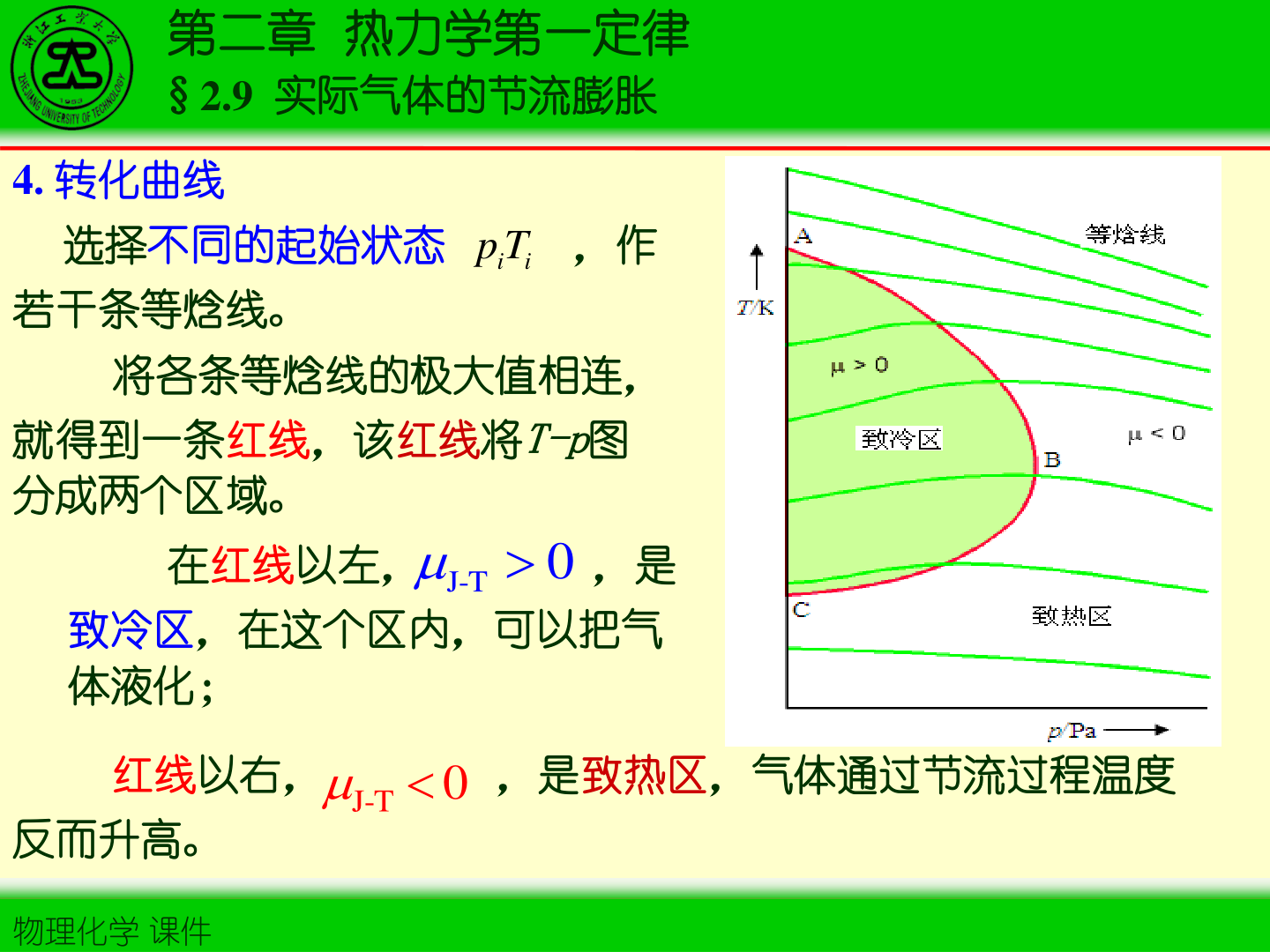
- μJ−T>0:节流后 T 降低(致冷)
- μJ−T<0:节流后 T 升高(致热)
- μJ−T=0:温度不变(转化温度点)
3. 转化温度与转化曲线
在 T-p 图上,μJ−T=0 的点连成转化曲线,将区域分成致冷区/致热区
4. 理想气体的特例
理想气体 H=H(T),等焓 ⇒T 不变
(IG) μJ−T=0
八、相变焓(§2.10)
1. 常见相变焓
- 熔化焓 ΔfusHm
- 汽化焓 ΔvapHm
- 升华焓 ΔsubHm
- 冷凝焓:ΔconHm=−ΔvapHm
2. 相变内能、相变功要点
- 凝聚相(熔化/冷凝/晶型转变等)常有 ΔV 很小,体积功近似为 0:
ΔH≈ΔU
- 蒸发/升华涉及气相体积变化,需考虑 pV 项(理想气体近似下常出现 ±ngRT 量级修正)

九、热化学基础(反应热,§2.11)
1. 反应进度(extent of reaction)
对反应
B∑νBB=0(νB>0 产物; νB<0 反应物)
定义反应进度 ξ:
ξ=νBnB(t)−nB(0)[ξ]=mol
微分形式:
dnB=νBdξ
2. 反应热与 ΔrU,ΔrH
- 恒容(量热弹)常对应 ΔrU;恒压常对应 ΔrH
3. ΔrH 与 ΔrU 的关系(理想气体近似)
ΔrH=ΔrU+ΔngRT
其中 Δng 为气体物质的量变化(按计量数求和)。
十、标准摩尔反应焓的计算(§2.12)
1. 标准态与标准摩尔反应焓
- 标准压力:p∘=100 kPa
- 标准摩尔反应焓:参与反应物质均处于各自标准态时,ξ=1 mol 的反应焓变,记作 ΔrHm∘(T)
2. 标准摩尔生成焓 ΔfHm∘
- 约定:最稳定单质的 ΔfHm∘=0
3. 由生成焓计算标准摩尔反应焓(常用公式)
ΔrHm∘(T)=B∑νBΔfHm,B∘(T)
十一、反应焓的温度校正:Kirchhoff 定律(常用结论)
1. Kirchhoff 定律(恒压)
dTd(ΔrH)=ΔrCp
其中
ΔrCp=B∑νBCp,m(B)
2. 积分形式(从 T1 到 T2)
ΔrH(T2)=ΔrH(T1)+∫T1T2ΔrCp(T)dT
十二、绝热反应(非等温反应,§2.13)
1. 核心思想(能量守恒)
- 绝热:与环境无热交换(Q=0)
- 反应放/吸出的热用于提升/降低体系温度(显热)
2. 典型能量衡算(示意写法)
ΔrH(T0)+B∑νB∫T0TCp,m(B,T)dT=0

速记清单(复习用)
- 第一律:ΔU=Q+W;δW=−pexdV
- 恒容(满足条件):QV=ΔU;恒压(满足条件):Qp=ΔH
- 焓:H=U+pV
- 热容:CV,m=(∂Um/∂T)V,Cp,m=(∂Hm/∂T)p
- 理想气体:U,H 仅与 T 有关;Cp,m−CV,m=R;γ=Cp/CV
- 绝热可逆:TVγ−1=const,pVγ=const
- 节流:ΔH=0;μJ−T=(∂T/∂p)H;转化曲线分致冷/致热
- 反应进度:dnB=νBdξ
- 反应焓/内能:ΔrH=ΔrU+ΔngRT(理想气体)
- 标准焓:p∘=100 kPa;ΔrHm∘=∑νBΔfHm,B∘
- Kirchhoff:d(ΔrH)/dT=ΔrCp






